< p0 > if exp then < p1 > stmt1 < p2 >
Please supply such equation templates for the live variable and available expressions problems. Briefly explain your answer.
SBuild the LR(0) and LR(1) machines for this grammar. Is the grammar LR(0), SLR(1), LALR(1), and/or LR(1). Briefly justify your answers.A a | b A c | d c | b d a
Ad
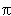 LALR of the LALR(1) machine for a grammar
G corresponds
to some state1,
LALR of the LALR(1) machine for a grammar
G corresponds
to some state1,
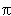 LR(0) of the LR(0) machine and that
the set of LR(1) items associated with each such
LR(0) of the LR(0) machine and that
the set of LR(1) items associated with each such 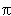 LALR is
described as:
LALR is
described as:
{ [ N
1 .
2 , x ] | for some state
LR(1) in the LR(1) machine, [ N

1 .
2 , x ]
LR(1) &
LR(0) = core(
LR(1) ) }
For this construction to make much sense, two conditions should hold:
- For each state,
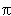 LR(0), of the LR(0) machine
there must be some state,
LR(0), of the LR(0) machine
there must be some state, 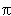 LR(1) in the LR(1)
machine such that
LR(1) in the LR(1)
machine such that 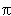 LR(0) = core(
LR(0) = core( 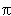 LR(1) )
LR(1) )
- For each state,
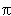 LR(1), of the LR(1) machine
it must be the case that core(
LR(1), of the LR(1) machine
it must be the case that core( 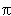 LR(1) ) is a
state of the LR(0) machine.
LR(1) ) is a
state of the LR(0) machine.
For this problem, I would like you to prove that one of these two conditions does hold. You are free to choose either a or b. Make your argument precise.
In your proof, you may assume the correctness of the central theorem that justified the correctness of LR(0) parsing (only half of which was actually proven in class):
Theorem:
[N -> 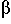 1 .
1 . 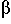 2 ]
2 ] 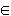
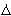 (
( 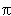 0,
0, 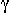 )
if and only if
[ N
)
if and only if
[ N

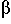 1 .
1 . 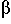 2 ] is valid for
2 ] is valid for 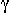 .
.
You may also assume the correctness of the corresponding theorem about LR(1) machines.
Theorem:
[N -> 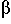 1 .
1 . 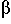 2, a ]
2, a ] 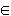
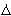 (
( 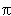 0,
0, 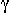 )
if and only if
[ N
)
if and only if
[ N

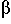 1 .
1 . 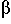 2, a ] is valid for
2, a ] is valid for 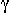 .
.
Of course, in the second theorem, "valid" means valid as an LR(1) item.
x = 27;
y = 81;
while x != y do
if x > y then
x = x - y
else
y = y - x
end
end