| Formal Grammars |
 ) is a finite,
possibly empty sequence of symbols from
) is a finite,
possibly empty sequence of symbols from  . We will
use eps to denote the empty string.
. We will
use eps to denote the empty string.
 , then
their concatenation, xy, is the sequence of characters obtained
by placing the sequence of characters in x before the sequence
y. If z = xy is a string, we say that x is a prefix of z
and y is a suffix of z.
, then
their concatenation, xy, is the sequence of characters obtained
by placing the sequence of characters in x before the sequence
y. If z = xy is a string, we say that x is a prefix of z
and y is a suffix of z.
{ xy | xX and y
y }
 we define Xn to be the language
containing only the empty
string if n = 0 and XXn-1 otherwise.
we define Xn to be the language
containing only the empty
string if n = 0 and XXn-1 otherwise.
 we define X+, the positive
closure of X, to be the union of the sets X1, X2, X3, . . .
and X*, the closure of X, to be the union of X0 and X+.
we define X+, the positive
closure of X, to be the union of the sets X1, X2, X3, . . .
and X*, the closure of X, to be the union of X0 and X+.
AX1 X2 . . . Xm
< stmt > -> while < expr > do < stmt >
< stmt > >= while < expr > do < stmt >
The "standard" interpretation is based on the next concept we consider, the derivation.
 A
A and
y =
and
y = 

 where
where
 ,
,  ,
, 
 (Vt U Vn)* and ( A,
(Vt U Vn)* and ( A,  )
)  P
we say that x directly derives y. In this case we write
P
we say that x directly derives y. In this case we write
xy
Consider G =
| < blob > |
 x < glob > < blob > y
x < glob > < blob > y | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| < blob > |
 z
z | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| < glob > |
 a < glob >
a < glob > | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| < glob > |
 eps
eps
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
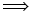 x < glob > < blob > y.
x < glob > < blob > y.
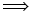 x a < glob > a
x a < glob > a
 0,
0,  1,
1,  2, ... ,
2, ... , m all in
(Vt U Vn)*
such that
m all in
(Vt U Vn)*
such that
 i
i
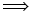
 i+1 ,
i+1 ,
 0 , and
0 , and
 m .
m .
xThe sequencey
 0,
0,  1,
1,  2, ... ,
2, ... , m is called a
derivation of length m of y from x.
m is called a
derivation of length m of y from x.
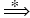 xaxzyy since:
xaxzyy since:
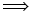 x < glob > < blob > y
x < glob > < blob > y
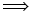 x a < blob > y
x a < blob > y
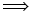 x a x < glob > < blob > y y
x a x < glob > < blob > y y
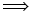 x a x < blob > y y
x a x < blob > y y
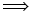 x a x z y y
x a x z y y
L(G) = { s | Ss & s
Vt* }
| Formal Grammars |