CS 334: HW 5
Instructions
This homework has three types of problems:
-
Self Check: You are strongly encouraged to think about and work through these questions, but you will not submit answers to them.
-
Problems: You will turn in answers to these questions.
-
Programming: You may work with a partner on it if you like.
Reading
- (Required) Read Mitchell, Chapters 6 and 7.
Problems
1. Type Inference (10 pts)
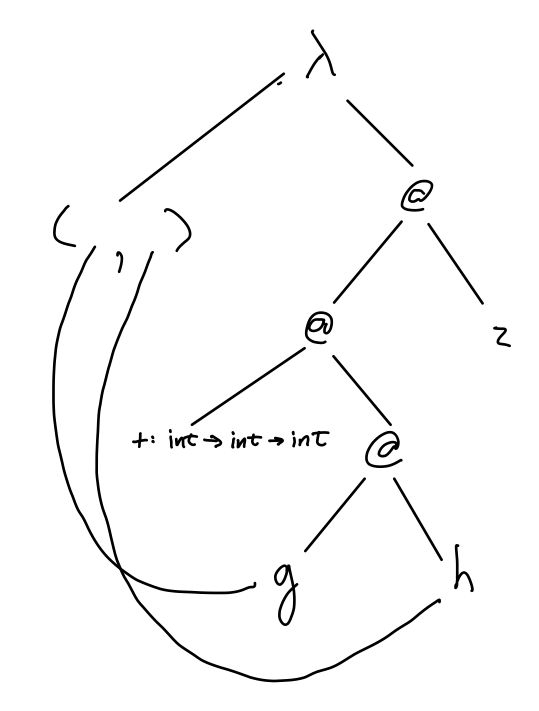
Infer the type for the following function using our type inference algorithm:
fun f(g,h) = g(h) + 2;
2. Type Inference to Detect Race Conditions (15 pts)
The general techniques from our type inference algorithm can be used to examine other program properties as well. In this question, we look at a non-standard type inference algorithm to determine whether a concurrent program contains race conditions. Race conditions occur when two threads access the same variable at the same time. Such situations lead to non-deterministic behavior, and these bugs are very difficult to track down since they may not appear every time the program is executed. For example, consider the following program, which has two threads running in parallel:
Thread 1: Thread 2:
t1 := !hits; t2 := !hits;
hits := !t1 + 1; hits := !t2 + 1;
Since the threads are running in parallel, the individual statements of Thread 1 and Thread 2 can be interleaved in many different ways, depending on exactly how quickly each thread is allowed to execute. For example, the two statements from Thread 1 could be executed before the two statements from Thread 2, giving us the following execution trace:
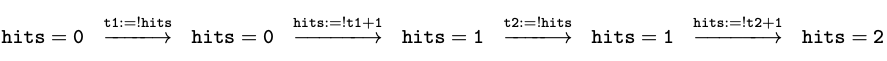
After all four statements execute, the hits
counter is updated from zero to 2, as expected. Another possible
interleaving is the following:
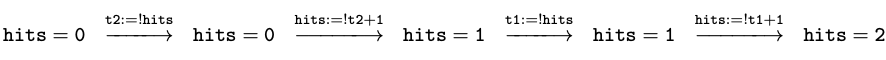
This again adds 2 to hits in the end. However,
look at the following trace:
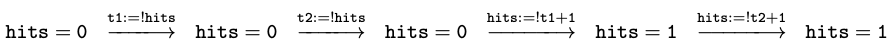
This time, something bad happened. Although both
threads updated hits, the final value is only 1. This is a race
condition: the exact interleaving of statements from the two threads
affected the final result. Clearly, race conditions should be
prevented since it makes ensuring the correctness of programs very
difficult. One way to avoid many race conditions is to protect
shared variables with mutual exclusion locks. A lock is an entity
that can be held by only one thread at a time. If a thread tries to
acquire a lock while another thread is holding it, the thread will
block and wait until the other thread has released the lock. The
blocked thread may acquire it and continue at that point. The
program above can be written to use lock l as follows:
Thread 1: Thread 2:
synchronized(l) { synchronized(l) {
t1 := !hits; t2 := !hits;
hits := !t1 + 1; hits := !t2 + 1;
} }
The statement "sychronized(l) { s }" aquires lock l, executes
s, and then releases lock l. There are only two possible
interleavings for the program now:

and
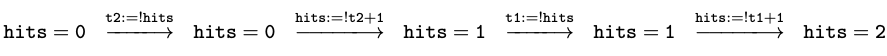
All others are ruled out because only one thread
can hold lock l at a time. Note that while we use assignable
variables inside the synchronized blocks, the names we use for locks
are constant. For example, the name l in the example program above
always refers to the same lock.
Our analysis will check to make sure that locks are used to guard shared variables correctly. In particular, our analysis checks the following property for a program P:
For any variable
yused in P, there exists some locklthat is held by the current thread every timeyis accessed.
In other words, our analysis will verify that every access to a
variable y will occur inside the synchronized statement for some
lock l. Checking this property usually uncovers many race
conditions.
Let's start with a simple program containing only one thread:
Thread 1:
synchronized (m) {
a := 3;
}
For this program, our analysis should infer that lock m protects
variable a.
As with standard type inference, we proceed by labeling nodes in the parse tree, generating constraints, and solving them.
Step 1
Label each node in the parse tree for the program with a variable. This variable represents the set of locks held by the thread every time execution reaches the statement represented by that node of the tree. Note that these variables keep track of sets of locks names, and NOT types, in this analysis.
Here is the labeled parse tree for the example:
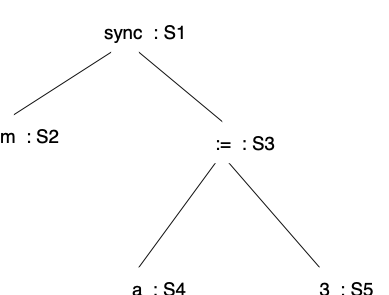
Step 2
Generate the constraints using the following four rules:
-
If S is the variable on the root of the tree, then S = \emptyset.
-
For any subtree matching the form
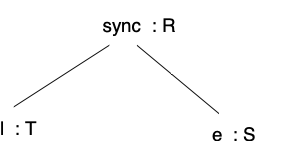
we add two constraints:
\begin{aligned} T & =& R\\ S & = & R \cup \{ {\tt l} \}\end{aligned} -
For any subtree matching the form
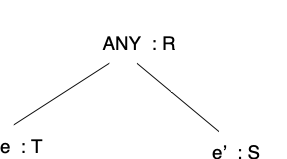
where ANY matches any node other than a
syncnode, we add two constraints:\begin{aligned} T & =& R\\ S & = & R \end{aligned} -
To determine {\tt lock_y}, the lock guarding variable {\tt y}, add the constraint
\begin{aligned} {\tt lock_y} & \in & S\end{aligned}for each node {\tt y}:S or {\tt !y}:S in the tree. In other words, require that {\tt lock_y} be in the set of locks held at each location {\tt y} is accessed.
Here are the constraints generated for the example program:
Step 3
Solve the constraints to determine the set of locks held at each program point and which locks guard the variables:
Clearly,
{\tt lock_a} is m in this case, exactly as we expected.
Questions
You will now explore some aspects of this analysis:
-
Here is another program and corresponding parse tree:
Thread 1: synchronized (l) { synchronized (m) { a := 4; b := !a; } b := 33; }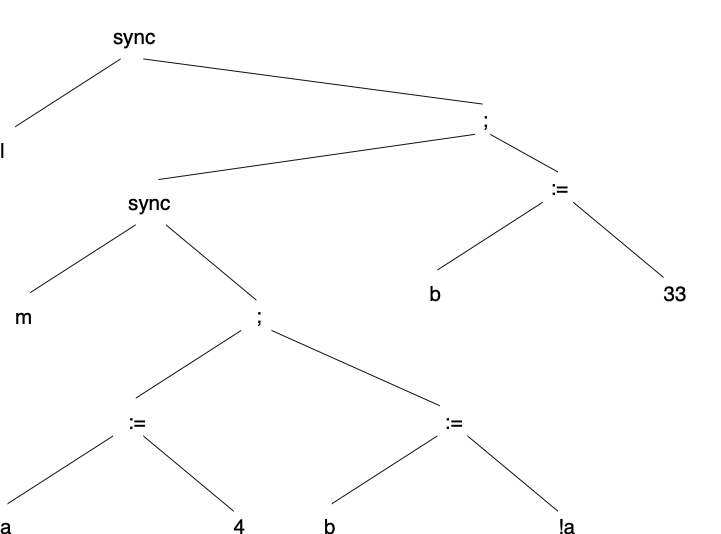
Compute {\tt lock_a} and {\tt lock_b} using the algorithm above. Explain why the result of your algorithm makes sense.
-
Let's go back to the original example, but change Thread 2 to use a different lock:
Thread 1: Thread 2: synchronized(l) { synchronized(m) { t1 := !hits; t2 := !hits; hits := !t1 + 1; hits := !t2 + 1; } }Compute {\tt lock_{t1}}, {\tt lock_{t2}}, and {\tt lock_{hits}} using the algorithm above. Since there are two threads in the program, you should create two parse trees, one for each thread. Explain the result of your algorithm.
-
Suppose that we allow assignments to lock variables. For example, in the following program,
landmare references to locks, and we can change the locks to which those names refer with an assignment statement:Thread 1: Thread 2: synchronized(!l) { synchronized(!m) { a := !a + 1; x := !b + 3 } b := 11 + x; m := !l; } synchronized(!m) { a := !b + 1; b := !a; }Describe any problems that arise due to assignments to lock variables, and what the implications for the analysis are. You do not have to show the constraints from this example or change the analysis to handle mutable lock variables. A coherent discussion of the issues is sufficient. Thinking about what the algorithm would compute for {\tt lock_a}, {\tt lock_b}, and {\tt lock_x} may be useful, however.
3. Parameter Passing (10 pts)
Mitchell, Problem 7.4
4. Swift Parameter Modes (20 pts)
This question explores parameter modes in the context of Apple's Swift language. We'll look at three modes: in, in-out, and out. Here is an example of each in Swift:
func test1(x: Int) -> Int { ... } /* default is "in" mode */
func test2(x: inout Int) -> Int { ... } /* "inout" mode */
func test3(x: out Int) -> Int { ... } /* "out" mode */
(Swift doesn't actually support the "out" mode, but other languages do, most notably Ada.) The three modes, have the following meaning:
- in: The value of the parameter x cannot be changed inside the function. If we call
test1(y), the value of y is the same before and after the call. - inout: The parameter x can be both read and written, and the value of y after a call to
test2(&y)is the last value written to x in the function. The&in the call to text2 is required by Swift to indicate that y is being passed as an in-out parameter. - out: The parameter x can be written to, but it cannot be read. If we call
test3(&y), the value of y after the call is the last value written to x in the function.
Questions
-
Why do you think the designers of Swift require the "
&" for in-out and out parameters at call sites? -
The language definition does not fully specify how each mode must be implemented, and the compiler may use any appropriate parameter passing mechanism to implement them.
Which parameter passing mechanism could be used to implement
test1,test2, andtest3? The choices are "pass-by-reference", "pass-by-value", and "pass-by-value-result" (as described in Problem 7.6). If more than one is possible, describe the advantages/disadvantages of each. -
In general, what is the advantage of permitting the compiler flexibility in how it implements parameter modes for such functions?
-
Now consider the following function that takes two parameters. Would the function
mainprint the same value for all strategies you outlined fortest2above? If it doesn't, why might that be problematic?func incTwo(a: inout Int, b: inout Int) { a += 1; b += 1; } func main() { var w : Int = 3; incTwo(&w, &w); print(w); } -
Swift disallows passing the same variable as two different in-out parameters, meaning the call to
incTwo(&w, &w)would be an error. Is this sufficient to avoid any problematic behavior identified in the previous part? There are alternative ways to achieve the same effect. Identify at least one. Why did you think the designers of Swift choose the option they did?
5. Static and Dynamic Scope (10 pts)
Mitchell, Problem 7.8
6. Function Returns and Memory Management (15 pts)
Mitchell, Problem 7.13
Note: g in the diagram in the book is a pointer and should have a dot next to it like the other pointers.
Programming
Folding Fun (30 pts)
Your GitLab account will have a "hw5" project for your to use for this question. You can follow the same instructions as on HW 1 for cloning it and adding a partner.
The "fold-left" (and "fold-right") functions appear in many
languages (as reduceRight/Left in Javascript, as accumulate in
C++, as foldl/foldr in ML, and so on.)
Here are their definitions in ML:
fun foldr f v nil = v
| foldr f v (x::xs) = f (x, foldr f v xs);
fun foldl f v nil = v
| foldl f v (x::xs) = foldl f (f(x, v)) xs;
Thus, foldr g b [a_0, ..., a_n] computes
g(a_0, g(a_1, g(a_2, ... g(a_{n}, b) ... )))
and foldl g b [a_0, ..., a_n] computes
g(a_{n}, g(a_{n-1}, g(a_{n-2}, ..., g(a_{0}, b) ... )))
The "fold-right" function reduces the elements in a list to a single value by repeated application of g, starting at the right of the list and working to the left. The "fold-left" function starts from the left and works to the right.
Here is an example usage, which defines a function sum that adds
together the numbers in a list:
- fun add(x,y) = x+y;
- fun sum elems = foldr add 0 elems;
- sum [2,3,4];
val it = 9: int
In effect, sum [2,3,4] computes
add(2, add(3, add(4, 0)))
Writing that function recursively would give us:
fun sum_rec nil = 0
| sum_rec (x::xs) = x + sum_rec(xs);
which computes the exact same value: sum_rec [2,3,4] computes 2
+ (3 + (4 + 0)). Many computations involve traversing a list and
computing a "summary" value for it. We explore other examples below,
and our folding operations enable us to write them in a succinct,
elegant way.
We could also define sum using foldl:
- fun sum2 elems = foldl add 0 elems;
in which case sum2 [2,3,4] computes
add(4, add(3, add(2, 0)))
Of course, we typically combine folding with anonymous functions, as
in the following definition of sum:
- fun sum elems = foldr (fn (x,result) => (x+result)) 0 elems;
The type of both foldr and foldl is
('c * 'd -> 'd) -> 'd -> 'c list -> 'd
That is, it takes as parameters a reducing function, an initial value, and a list. It produces a single summary value.
-
Using a fold operation, write a function
concatWords: string list -> string. This function should return return a string with all strings in the list concatenated:- concatWords nil; val it = "" : string - concatWords ["Three", "Short", "Words"]; val it = "ThreeShortWords" : string -
Using a fold operation, write a function
wordsLength: string list -> int. This function should return the total length of all words appearing in a list of strings. For example:- wordsLength nil; val it = 0 : int - wordsLength ["Three", "Short", "Words"]; val it = 15 : int -
Can we always use
foldlin place offoldr? If yes, explain. If no, give an example functionf, listl, and initial valuevsuch thatfoldr f v landfoldl f v lbehave differently. -
Using a fold, write a function
count: ''a -> ''a list -> int. It computes the number of times a value appears in a list. For example:- count "sheep" ["cow", "sheep", "sheep", "goat"]; val it = 2 : int - count 4 [1,2,3,4,1,2,3,4,1,2,3,4]; val it = 3 : int -
Using a fold, write a function
partition: int -> int list -> int list * int listthat takes an integer p and a list of integers l, and that returns a pair of lists containing the elements of l smaller than p and those greater than or equal to p. The ordering of the original list should be preserved in the returned lists. (We wrote a recursive form during lecture as part of quicksort.)- partition 10 [1,4,55,2,44,55,22,1,3,3]; val it = ([1,4,2,1,3,3],[55,44,55,22]) : int list * int list -
Using a fold, write a function
poly: real list -> (real -> real)that takes a list of reals c[a_0, a_1, ..., a_{n-1}] and returns a function that takes an argumentband evaluates the polynomiala_0 + a_1 x + a_2 x^2 + \cdots + a_{n-1} x^{n-1}at x = b; that is, it computes \sum_{i=0}^{n-1} a_i b^i. For example,
- val g = poly [1.0, 2.0]; val it = fn: real -> real - g(3.0); val it = 7.0: real - val g = poly [1.0, 2.0, 3.0]; val it = fn: real -> real - g(2.0); val it = 17.0: realHint
a_0 + a_1 x + a_2 x^2 + a_3 x^3 = a_0 + x (a_1 + x (a_2 + x a_3)). This is an example of Horner's Rule. Horner's Rule demonstrates that we can evaluate a degree n polynomial with only O(n) multiplies.
Submitting Your Work
Submit your homework via GradeScope by the beginning of class on the due date.
Written Problems
Submit your answers to the Gradescope assignment named, for example, "HW 1". It should:
- be clearly written or typed,
- include your name and HW number at the top,
- list any students with whom you discussed the problems, and
- be a single PDF file, with one problem per page.
You will be asked to resubmit homework not satisfying these requirements. Please select the pages for each question when you submit.
Programming Problems
If this homework includes programming problems, submit your code to the Gradescope assignment named, for example, "HW 1 Programming". Also:
- Be sure to upload all source files for the programming questions, and please do not change the names of the starter files.
- If you worked with a partner, only one of each pair needs to submit the code.
- Indicate who your partner is when you submit the code to gradescope. Specifically, after you upload your files, there will be an "Add Group Member" button on the right of the Gradescope webpage -- click that and add your partner.
Autograding: For most programming questions, Gradescope will run an autograder on your code that performs some simple tests. Be sure to look at the autograder output to verify your code works as expected. We will run more extensive tests on your code after the deadline. If you encounter difficulties or unexpected results from the autograder, please let us know.
